 i4.1.1
i4.1.1  i4.2.1
i4.2.1 
Updated 24th February, 2021
A labelled peer code may used to describe a link immersion, that is a map from a number of disjoint circles to the plane with no triple or higher multiple points, where the image of each circle is called a component. A link immersion with one component is sometimes referred to as a knot shadow.
An example of a labelled peer code for an immersion of a link with two components and five crossings is [-9 -5 7, -1 3]/# # # # #. Every link immersion may be described by a (non-unique) labelled peer code but not every labelled peer code corresponds to a link immersion in the plane; that is, not every labelled peer code is realizable.
Labelled peer codes easily lend themselves to enumeration by computer and realizable codes are readily identified. Moreover, it is possible to identify those realizable codes that correspond to a connected sum of two simpler immersions. This approach therefore gives a way to identify every possible link immersion. The prime immersions are the more interesting from the perspective of classification, though in general connected sums may be distinct and interesting in their own right, in some theories. This page presents the results of a search for both prime and non-prime immersions. In the course of the enumeration, it is easy to identify those peer codes describing an immersion that contains a Reidemeister I (monogon) configuration and these codes are ignored, since monogons introduce an infinite variety that is not considered by most knot theories.
The labelled immersion code for a given diagram is clearly not unique but it is a straightforward matter to prune an initial list of realizable codes by removing renumbering equivalents (including orientation reversal) of both individual components and, for links, numbering components in different orders.
The following table shows the number of realizable peer codes corresponding to distinct link immersions for manageable numbers of crossings and components:
| number of crossings, n | number of components, m | |||||||
|---|---|---|---|---|---|---|---|---|
| prime | prime and non-prime | |||||||
| m=1 | m=2 | m=3 | m=4 | m=1 | m=2 | m=3 | m=4 | |
| 3 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 4 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 |
| 5 | 2 | 1 | 0 | 0 | 2 | 2 | 1 | 0 |
| 6 | 3 | 4 | 2 | 0 | 5 | 8 | 5 | 3 |
| 7 | 10 | 7 | 1 | 0 | 16 | 20 | 17 | 4 |
| 8 | 27 | 27 | 7 | 1 | 52 | 95 | 72 | 28 |
| 9 | 101 | 77 | 19 | 1 | 205 | 369 | 312 | 137 |
| 10 | 364 | 341 | 843 | 1759 | ||||
| 11 | 1610 | 3897 | ||||||
The following pages present the labelled peer codes corresponding to the above table:
Prime Immersions
All Immersions (including non-prime)
The above lists were calculated using the programme vlist, which is available as a source distribution here: vlist-release-10-11-20.tar
The lists of prime and non-prime immersions were generated using command lines either of the form vlist -i n m to calculate immersions of up to n crossings having m components, or of the form vlist -ix n m to calculate immersions of exactly n crossings and m components. The lists of just prime immersions were calculated by adding the P option, as in vlist -iP n m
Below we provide diagrams of prime link immersions, rendered from the above labelled peer codes by the draw programme.
Realizable immersions provide a starting point for searching for a variety of classes of knots and links, such as welded knots, and both planar and virtual doodles.
Prime immersions with less than six crossings
i3.1.1  i4.1.1
i4.1.1  i4.2.1
i4.2.1 
i5.1.1  i5.1.2
i5.1.2  i5.2.1
i5.2.1 
Immersions with six crossings and one component
i6.1.1  i6.1.2
i6.1.2  i6.1.3
i6.1.3 
Immersions with six crossings and two components
i6.2.1  i6.2.2
i6.2.2  i6.2.3
i6.2.3 
i6.2.4 
Immersions with six crossings and three components
i6.3.1  i6.3.2
i6.3.2 
Immersions with seven crossings and one component
i7.1.1  i7.1.2
i7.1.2  i7.1.3
i7.1.3 
i7.1.4  i7.1.5
i7.1.5 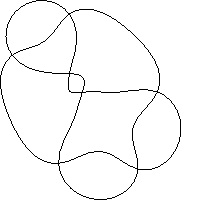 i7.1.6
i7.1.6
i7.1.7  i7.1.8
i7.1.8  i7.1.9
i7.1.9 
i7.1.10
Immersions with seven crossings and two components
i7.2.1  i7.2.2
i7.2.2  i7.2.3
i7.2.3 
i7.2.4  i7.2.5
i7.2.5  i7.2.6
i7.2.6 
i7.2.7 
Immersions with seven crossings and three components
i7.3.1 
Immersions with eight crossings and one component
i8.1.1  i8.1.2
i8.1.2  i8.1.3
i8.1.3 
i8.1.4  i8.1.5
i8.1.5  i8.1.6
i8.1.6 
i8.1.7  i8.1.8
i8.1.8  i8.1.9
i8.1.9 
i8.1.10  i8.1.11
i8.1.11  i8.1.12
i8.1.12 
i8.1.13  i8.1.14
i8.1.14 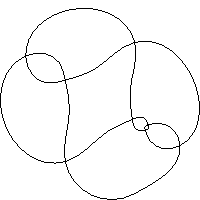 i8.1.15
i8.1.15 
i8.1.16  i8.1.17
i8.1.17  i8.1.18
i8.1.18 
i8.1.19  i8.1.20
i8.1.20  i8.1.21
i8.1.21 
i8.1.22  i8.1.23
i8.1.23  i8.1.24
i8.1.24 
i8.1.25  i8.1.26
i8.1.26  i8.1.27
i8.1.27 
Immersions with eight crossings and two components
i8.2.1  i8.2.2
i8.2.2  i8.2.3
i8.2.3 
i8.2.4  i8.2.5
i8.2.5  i8.2.6
i8.2.6 
i8.2.7  i8.2.8
i8.2.8  i8.2.9
i8.2.9 
i8.2.10  i8.2.11
i8.2.11  i8.2.12
i8.2.12 
i8.2.13  i8.2.14
i8.2.14  i8.2.15
i8.2.15 
i8.2.16  i8.2.17
i8.2.17  i8.2.18
i8.2.18 
i8.2.19 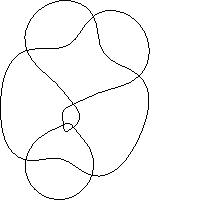 i8.2.20
i8.2.20  i8.2.21
i8.2.21 
i8.2.22  i8.2.23
i8.2.23  i8.2.24
i8.2.24 
i8.2.25  i8.2.26
i8.2.26  i8.2.27
i8.2.27 
Immersions with eight crossings and three components
i8.3.1  i8.3.2
i8.3.2  i8.3.3
i8.3.3 
i8.3.4  i8.3.5
i8.3.5  i8.3.6
i8.3.6 
i8.3.7 
Immersions with eight crossings and four components
i8.4.1 
Immersions with nine crossings and one or two components
These have been omitted due to their large number.
Immersions with nine crossings and three components
i9.3.1  i9.3.2
i9.3.2  i9.3.3
i9.3.3 
i9.3.4 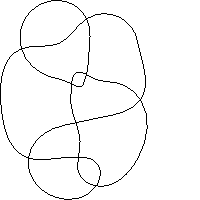 i9.3.5
i9.3.5  i9.3.6
i9.3.6 
i9.3.7  i9.3.8
i9.3.8  i9.3.9
i9.3.9 
i9.3.10  i9.3.11
i9.3.11  i9.3.12
i9.3.12 
i9.3.13  i9.3.14
i9.3.14  i9.3.15
i9.3.15 
i9.3.16  i9.3.17
i9.3.17  i9.3.18
i9.3.18 
i9.3.19 
Immersions with nine crossings and four components
i9.4.1 